In this post, I will go over my implementation of ‘A Neural Algorithm of Artistic Style’ and explain my understanding of it.

I was pleasantly surprised to find how easily this paper explains the process. So basically authors say that its possible to separate style and content representation of an image using a pretrained model. They use this insight to create visually pleasing images by transferring style of one image to content of another image. So now there are 2 parts for style transfer - Reconstruction of content, Reconstruction of style to convince ourselves that its possible to get only the content or only style from an image using a CNN model.

Before the reconstruction we need to take a pre-trained model (authors have used VGG19, but since I have only 4GB graphics card, I went with VGG16) and modify it to be able to output from any intermediate layer.

class VGG16(torch.nn.Module):
    def __init__(self, content_layer = 'relu4_3', 
                style_layers = ['relu1_2', 'relu2_2', 'relu3_3', 'relu4_3']):
        super().__init__()
        self.vgg16 = models.vgg16(pretrained=True).requires_grad_(False).features
        self.form_layers()
        ....

    def form_layers(self):
        self.layers = {}
        block = 1
        conv_index = 1
        relu_index = 1
        for index, layer in enumerate(self.vgg16):
            name = layer.__class__.__name__
            if name == 'Conv2d':
                self.layers[f'conv{block}_{conv_index}'] = index
                conv_index += 1
            elif name == 'ReLU':
                self.layers[f'relu{block}_{relu_index}'] = index
                relu_index += 1
            elif name == 'MaxPool2d':
                max_pool = self.vgg16[index]
                self.vgg16[index] = nn.AvgPool2d(kernel_size=max_pool.kernel_size, stride=max_pool.stride,
                                        padding=max_pool.padding, ceil_mode=max_pool.ceil_mode)
                self.layers[f'pool{block}'] = index
                block += 1
                conv_index = 1
                relu_index = 1
            else:
                print('Something is wrong!!!')

    def forward(self, x):
        .....
        return (content_feature_map, style_feature_maps)

So here I gave a name to each layer so that its easy to access using the conventional notation such conv1_1, conv2_1 etc. And also in the paper the authors mention that they saw better results with Average pooling than Max pooling, so I replaced all Max pooling layers with Average pooling while retaining all the common parameters.

class VGG16(torch.nn.Module):
    def __init__(self, content_layer = 'relu4_3', 
                style_layers = ['relu1_2', 'relu2_2', 'relu3_3', 'relu4_3']):
        super().__init__()
        self.vgg16 = models.vgg16(pretrained=True).requires_grad_(False).features
        ...
        self.content_layer = content_layer
        self.style_layers = style_layers

        for p in self.parameters():
            p.requires_grad = False


    def forward(self, x):
        content_feature_map = None
        style_feature_maps = []

        style_index = 0
        for name, index in self.layers.items():
            x = self.vgg16[index](x)
            if name == self.content_layer:
                content_feature_map = x
            
            if style_index < len(self.style_layers) and name == self.style_layers[style_index]:
                style_index += 1
                style_feature_maps.append(x)

        
        return (content_feature_map, style_feature_maps)

Depending on what content layers and style layer names are required, outputs from corresponding layers are stored and returned in forward call.

Reconstruction of Content

This is the easier of the two. In this, the idea is that the layers of model capture the content at different levels of abstraction. In the sense that the earlier layers capture only the basic details like lines and corners. And as we go to higher levels, the layers capture more meaningful and abstract details, like shape of house or its alignment.

To reconstruct the content, we take a content image (target, which we want to achieve) and a random data image (Could be guassian noise) and use a pre-trained model to get the output of any of the layers as features from both. Then we modify the noise image until the squared error between the feature vectors of content image and noise image is minimised.

$$\text{Loss}_{content} = \frac{1}{2} \sum (\text{Features}_{content} - \text{Features}_{noise})^2$$

def get_content_loss(
    image_features: torch.Tensor, target_features: torch.Tensor
) -> torch.Tensor:
    mse_loss = nn.MSELoss()
    return mse_loss(image_features, target_features)

Note: Here we dont modify the weights of the model, but only the noise image using backpropagation.

Reconstruction of Style

To reconstruct the style we take output from multiple layers and calculate Gram matrix for each. Gram matrix is basically a co-variance matrix of each of the feature vectors in the output of a layer. We consider Gram matrices of multiple layers, lets say L for both the Style image (target, the image style we want to recreate) and a noise image. Now similar to before, we find the difference between the gram matrices of style image and noise image using the loss

$$E_l = \frac{1}{4 \cdot N_l^2 \cdot M_l^2} \sum_{i,j} (\text{Gram Matrix}_{i,j}^{style} - \text{Gram Matrix}_{i,j}^{noise})$$

for each layer and combined as

$$\text{Loss}_{style} = \sum_{l=0}^L w_l E_l$$

where N is no of the features / filters in a particular layer and M is the product of height and width of feature map. And authors have taken w to be (1 / No of layers) that are considered to get the output.

def construct_gram_matrix(feature_map: torch.Tensor) -> torch.Tensor:
    gram_matrix = feature_map @ feature_map.T
    return gram_matrix

def get_style_loss(
    image_features: torch.Tensor, target_gram_matrices: List[torch.Tensor]
) -> torch.Tensor:
    loss = 0.0
    for i, feature in enumerate(image_features):
        feature = feature.squeeze()
        noise_feature_map = feature.view(feature.shape[0], -1)
        noise_gram = construct_gram_matrix(noise_feature_map)

        layer_loss = torch.sum(torch.square((target_gram_matrices[i] - noise_gram))) / (
            4 * (feature.shape[0] ** 2) * (feature.shape[1] ** 2)
        )
        loss += layer_loss / len(image_features)

    return loss

Style Transfer

Now that we have the reconstruction of style and content, we can mix both to get an image, which minimizes both the errors at the same time and in a sense obtain an image which is having content from a content image and style from style image. We obtain the both content features and style features from a starting image and optimize this w.r.t to content features from content image and style features from style image. The combined loss is defined as

$$\text{Total Loss} = \alpha \text{Content Loss} + \beta \text{Style Loss}$$

Authors have used ⍺ and ꞵ as weighting factors with ratio ⍺/ꞵ = 1e-3 or ⍺/ꞵ = 1e-4. I tried with different ratios but didnt really find a lot of differences in my output. Another important factor is the starting image. While using either a noise image or the style image itself as starting image, the output couldnt fully capture the content of the image and only style was properly transferred. So starting with the content image produced the most visually pleasing result in my implementation.

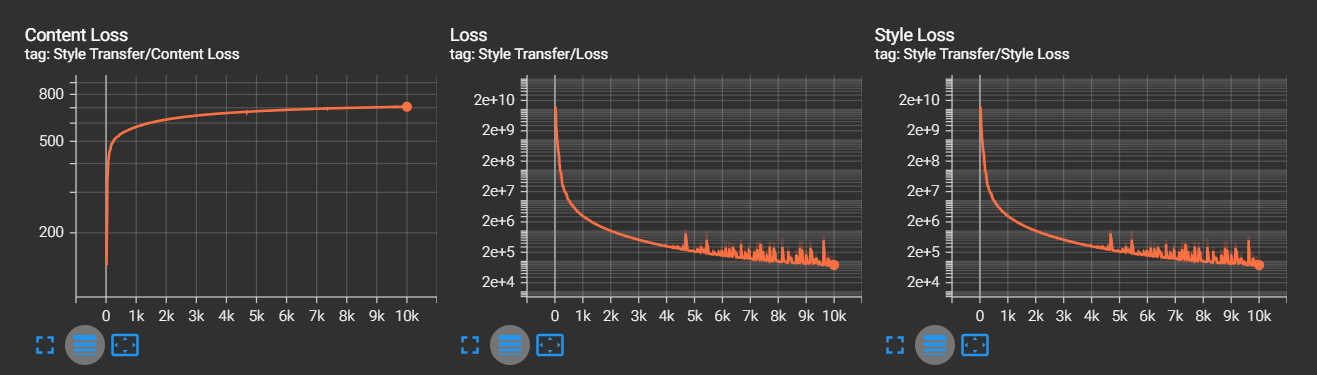
I used Adam optimizer with starting learning rate of 1 and a step decay. The loss falls off steeply in the beginning so its fine to have high learning rate initially. I did notice some unsteadiness in loss curve towards the end of the training, probably pointing to a relatively high learning rate at that stage, so a higher decay rate might be a good option.

def style_transfer(
    content_image: torch.Tensor, style_image: torch.Tensor, start_type: StartingImage
) -> None:
    global writer
    ...

    target_content_features, _ = model(content_image)
    target_content_features = target_content_features.squeeze()

    _, target_style_features = model(style_image)
    target_style_grams = []
    for feature in target_style_features:
        feature = feature.squeeze()
        target_style_feature_map = feature.view(feature.shape[0], -1)
        target_style_grams.append(construct_gram_matrix(target_style_feature_map))

    for epoch in range(EPOCHS + 1):
        content_features, style_features = model(image)
        content_loss = get_content_loss(
            content_features.squeeze(), target_content_features
        )
        style_loss = get_style_loss(style_features, target_style_grams)
        total_loss = (CONTENT_WEIGHT * content_loss) + (STYLE_WEIGHT * style_loss)

        total_loss.backward()
        optimizer.step()
        optimizer.zero_grad()
        lr_scheduler.step()
        ...

Loss curves

Output

Conclusion

This was a fun paper to implement without a lot of complicated stuff. But it also intorduced a new concept (to me) of modifying the image itself instead of model weights. This is also quite an old paper and there have been a lot of research on this where people have optimized a model to generate the image instead of optimizing error with respect to image itself and lot of different ways to control the output. A nice blog mentions some of them briefly - https://www.fritz.ai/style-transfer/

References

Paper: ‘A Neural Algorithm of Artistic Style’
Github: https://github.com/Suhas-G/computer-vision/neural-style-transfer